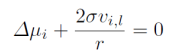终于进入到了气体和液体共同存在的体系,距离我们讨论气泡也越来越近了。但此之前,我们需要先了解当气体和液体共存时的现象和基础理论知识。首先我们从了解热力学平衡态开始。研究和描述气体和液体共存体系平衡的过程称为气液相平衡(Vapor-Liquid Equilibrium, VLE),这里之所以是Vapor,因为最简单的气液相平衡体系的气相是由液相蒸汽构成的,整个体系只有一种物质。
气液相平衡描述了在一定温度、压力下,气相与液相共存时,系统中各组分在两相中浓度不再随时间变化后的动态平衡状态,其本质是分子在气液两相间的迁移速率达到平衡,即相同时间内从液相逸出到气相的某组分分子数,等于从气相溶解进入液相的某组分分子数,宏观上表现为两相组成、温度、压力等保持恒定。
液相分子的逸出:液相中,分子间存在范德华力(极性分子还存在氢键),束缚分子的自由运动;但部分分子因热运动获得高于 “逸出能垒” 的动能,可克服分子间作用力从液相表面逸出,进入气相。温度越高,分子平均动能越大,能克服能垒的分子比例越高,逸出速率越快。 气相分子的溶解:气相中,分子做无规则扩散运动,部分分子会与液相表面碰撞并被液相分子的作用力捕获,重新进入液相。
气相压力越高,单位体积内的分子数越多,碰撞液相表面的频率越高,溶解速率越快。 两者速率相等时,气相组成(分压)和液相组成不再变化,系统达到气液相平衡。 由于气液相平衡对于后续成核理论,气泡的形成非常重要,我们需要略微增加理论深度,以保证后续知识的理解。 首先,我们考虑一个隔离箱,包括气相区和液相区,以及两者之间的一个平面s(恒定面积A,厚度忽略不计)隔开,下标代表对应区域。如果我们通过一个可逆过程移动平面,则三个区域的熵变可以表示为:
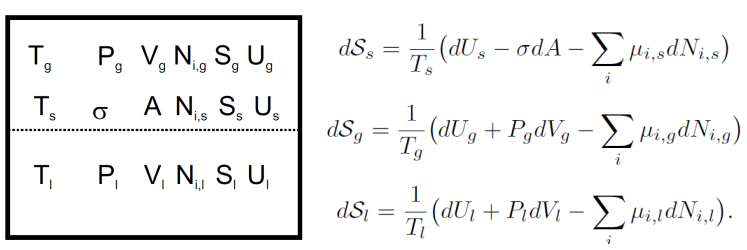
由于整个体系为隔离体系,因此:
![]()
此外,由于体系在整个过程中内能U,分子量n和体积V没有发生变化,我们把这三个守恒条件、总熵变和界面面积A变化为零一起带入,,得到
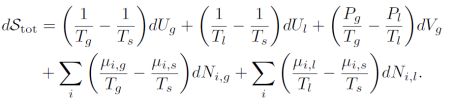
由于上式为零,对于全微分,系数应均为零,可以得到
![]()
即三个区域温度相等,化学势相同(即分子进入三个区域所需的能量相同)。
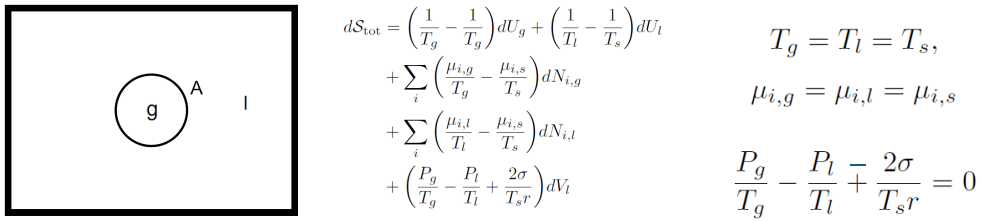
对于一个气泡,和上述推导相似,我们可以得到 注意下标和力的方向
下一步,进行一个麦克斯韦变换,并定义物质i的偏摩尔体积:
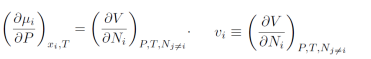
对所有组分求和得到,且第二项必须为零:
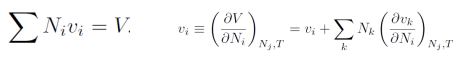
此外,当xi和T不变时,我们从上面的公式可以得到,再对液体i组分化学潜势积分,再把压力和表面张力关系带入:
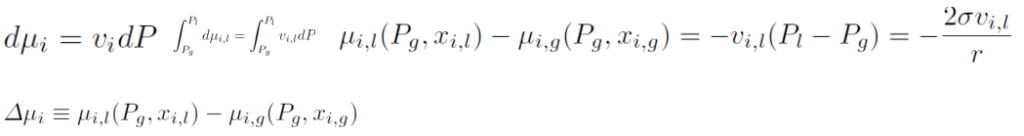
得到开尔文公式(这个在胶体稳定性部分会用到):