热力学通过判断过程的吉布斯自由能等参数的变化,看预测过程的自发性,即是否可以发生;而动力学则主要研究可能发生过程的演变速度,在实际工程应用中,由于可以改变过程条件,如加压、升温等,迫使过程向希望的方向进行,因此对热力学的关注往往较少,而更多的关注这个过程进行的速度,这直接影响经济效益,因此对动力学的关注往往更多,如化学反应、传质扩散等。根据针对过程的不同,动力学可以分为反应动力学(化学反应速率)、扩散动力学(物质迁移速率)、相变动力学(如气泡形成过程)等,作为关注气泡的我们,对气液传质扩散动力学和气泡形成过程的成核动力学最为关注,这两方面的内容我们把它们分别放到气液传质和成核理论中去讨论,这里主要了解动力学的一些基础知识。
动力学的研究和很多其他领域的研究一样,首先通过宏观实验现象建立数学模型,然后再根据模型以及微观粒子统计力学行为的方式来推断机理,建立基础理论。 动力学研究中,当其他条件不变时,反应速度与反应物浓度之间的关系一般都可以表述为:
![]()
其中m+n成为总反应级数,例如m=n=0时,称为零级反应,n=0,m=1时,称为一级反应,m=n=1时称为二级反应。
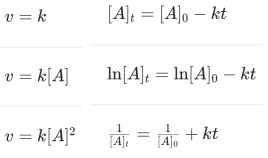
很多关注微纳米气泡的环保领域的客户一定对反应动力学非常了解,因为COD、特定有机物的氧化分解过程,一般都会默认氧化物或目标物在过程中浓度不变,将动力学转化为准一级反应动力学进行研究。 对于关注气泡的我们,受温度影响的阿伦尼乌斯方程更需要了解,这里引入了活化能Ea,实际上这算是一个分子级的“概率屏障”。这个指数形式的方程我们在成核和传质过程中还会遇到。对于反应过程,我们可以根据平衡条件下的动力学和热力学方程将活化能和热力学参数焓建立联系,即
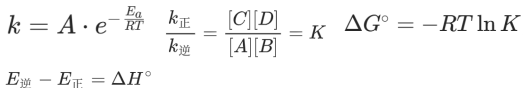
任何宏观过程的动力学,其本质都是是微观粒子的运动与相互作用频率决定的。无论是反应级数还是温度关联性,动力学机理和表观速率之间的关系通过碰撞理论建立起来,路易斯(W.C. Lewis)提出有效碰撞理论,反应物分子之间无时无刻不在发生 “碰撞”,当满足两个条件的 “有效碰撞” 导致反应,第一是能量条件,即碰撞分子的总能量 ≥ 反应的 “活化能Ea”(克服分子间电子排斥、断裂旧键所需的最低能量);第二是取向条件,碰撞分子的空间取向合适,显然这样的碰撞会导致反应速率 ∝正比于单位时间有效碰撞次数,而有效碰撞次数与 “活化分子分数”(能量≥Ea的分子占比)、“碰撞频率”(单位体积内分子碰撞次数)正相关,此外,埃林(H. Eyring)等人提出的过渡态理论,提出反应存在高能中间产物,这个高能中间产物与反应物的能力差值极为活化能。
![]()
