由于我们所讨论的气泡存在于液体(主要是水)中,在了解完气体的一些基础理论后,我们再来了解一下液体。
正像范德华所说的一样,气体和液体没有本质区别,只是分子间作用力不同而已,但是,即使对于最简单的液体也没有形成一个真正的分子理论。 我们只能这样含糊的描述来略微区分一下液体和气体、固体的区别: 假设我们有一大群分子,而我们已经充分掌握了其中一个分子的详细信息,如运动状态等,那么我们能推断多少其他分子的信息? 如果这一大群分子是气体分子,我们几乎什么也推断不了; 如果这一大群分子是液体分子,我们可以大致推断出其他分子的部分信息; 如果这一大群分子是固体分子,我们几乎可以全部推断出其他分子的全部信息。 换句话说,液体是一种聚集态,其结构与性质兼具 “短程有序、长程无序” 的特征,但需要注意的是,对于水,这种如此特殊的液体,其在某种程度上具体长程有序的特征(这有说明长程无序不应是液体的普遍特征)。
咱们还是关注液体在宏观表现吧。
2.1 液体流动
首先,我们先了解一点基本的流体力学知识。在早期的静压强公式中,帕斯卡就指出密闭流体中,施加于任意点的压强将等值、均匀地传递到流体的所有部分(实际上,这种表述默认了液体连续性,即在分析的空间尺度内液体没有结构,是“致密” 的)。
![]()
伯努利的理想流体宏观方程从能量守恒、动量守恒出发,解释了流量压力、重力势能和动能的相互转化,这也是文丘里、射流器等水利设备的设计基础。
![]()
液体分子可自由滑动,但由于液体分子间的吸引力会阻碍滑动,表现为 “粘滞性”(粘度),在欧拉将理想流体运动数学化的基础上,流体力学的基础方程——纳维- 斯托克斯方程诞生,标志着基于连续介质力学方法描述黏性流体运动成为可能(对于计算流体力学以及量子力学,会有很多算子帮助简化方程,要有基础的了解)。
![]()
为了随后空化和气液两相流的介绍需要,这里我们再多了解一些流体力学知识。
(1)层流和湍流
层流与湍流是指流体运动的 “两种形态”,湍流的本质是流体能量耗散的强化。把人看流体的组成部分,层流很像走过天安门前的阅兵队伍的“流动”,对任何一个人来说,他永远追不上他前面的人,也永远不会被后面的人追上,同时他的左右永远都是同一个人,人和人之间也不会有碰撞发生,从天安门城楼上看下去,是一种整齐、规则的“流动”,如果让所有人都身着白色,而仅其中一个人身着黑色,那这个“黑点”的运动轨迹就是茫茫白色中的一条直线;而湍流就像上下班高峰期涌向地铁门口的乘客“流动”,对任何一个人来说,他可能被挤的往后、往左、往右,但总体上是在往前,不知道会碰上那个人,也不知道碰到的那个人是往哪个方向的,从自动扶梯上往站台看,是一种混乱、令人烦躁的“流动”,如果让所有人都身着白色,而仅其中一个人身着黑色,那这个“黑点”的运动轨迹就是茫茫白色上的一团“乱麻”。我们再稍微多想一下,如果这个黑衣人是一个猥琐男,我们把他每次碰到一个白衣美少女的过程看做是该部分流体(黑衣猥琐男)和其他部分流体(白衣美少女)的一次传热(热交换)、传质(物质交换)的过程,那么显然,对该部分流体(猥琐男)而言,挤地铁比天安门前阅兵来说要有利的多,这也是为什么传热、传质(比如想尝试使用微纳米气泡提高传质效率的客户,如养殖增氧、生物池曝气、催化加氢、氦洗等)过程都往往存在湍流的原因,这就需要一定程度掌握层流和湍流的转变条件、湍流的宏观特征(如不规则性、扩散性、能量耗散),这些我们在气液传质理论部分在深入了解。
(2)边界层
在利用微纳米气泡减少流动阻力、提升清洗效果等应用场景时,其作用机理往往发生在边界层内,如边界层扰动等,因此我们需要稍微了解一下边界层的概念。 边界层是指流体流经固体壁面时,由于粘性作用,就是固体对流体分子有吸引力,不让流体分子离开,导致贴紧壁面的这层流体分子(我们暂时称为0层分子)速度为 0,下一层流体分子(1层分子)由于和0层流体分子之间也有吸引力,但吸引力毕竟没那么强,导致1层分子速度下降,但没有下降为零,同样的,2层、3层…的流体分子速度就越来越快,直到当n层和n+1流体分子相同时,那么n+1以后层的流体分子速度就不会在发生变化了,我们把0层到n层的流体分子所在的区域就叫做边界层。
(3)斯托克斯公式
斯托克斯推导了标准球体在黏性流体中运动时受到的阻力,r 为物体半径,v 为物体与流体的相对速度。该公式是 “斯托克斯流”,这是微米级气泡在静流体中受到的粘滞阻力和流速的关系,因为在地球上微米气泡还受到浮力,所以一个微米气泡在静止的水中形成后,由于没啥速度,Fd也就为零,只受浮力,开始上升,一旦产生速度,就开始产生粘滞阻力,加速过程放缓,直到浮力等于Fd后,气泡受力平衡,竖直方向匀速直线运动上浮,也就是我们常说的气泡上升速度,近似于我们看到白色不断上升的“乳白色” 微米气泡,也就是为什么我们大致可以根据白色消失的速度来大致判断气泡的大小。
![]()
(4)涡街
涡街是流体流经钝体(如圆柱、球体)时,边界层分离后形成的交替排列的涡旋列,分为稳定周期性“卡门涡街”(稳定涡街)和不规则“非定常涡街”,涡街流量计就利用了这个原理。另一方面,气液传质理论中的表面更新理论本质就是涡旋和局部湍流驱动的非稳态分子扩散,NANOscientific的源技术——Multi-Vortex技术正是利用了湍流场多重涡街强化气液传质效率的,这些在气液两相流部分我们还会提到。
(5)无量纲数
在流体力学中,无量纲数是描述流体运动特性、简化方程、判断流动相似性的核心工具。它们通过将物理量(如速度、长度、密度、黏度等)组合成无单位的比值,消除了具体物理量的量级影响,仅保留流动的本质特征(如惯性力、黏性力、表面张力、重力等的相对重要性),对于关注气泡的我们,常用的到无量纲数包括雷诺数(Reynolds Number, Re),表示惯性力 / 黏性力的比值
![]()
施密特数(Schmidt Number, Sc),动量扩散率 / 质量扩散率的比值
![]()
韦伯数(Weber Number, We),惯性力 / 表面张力的比值
![]()
斯特劳哈尔数(Strouhal Number, St),特征频率对应的时间尺度 / 流动通过特征长度的时间尺度的比值
![]()
空化数(Cavitation number, σ),“阻止空化的压力差” 与 “流动动压” 的比值,反映空化的难易程度
![]()
实际上,基于加压溶解减压释放过程的微纳米气泡过程,从热力学和动力学上虽然有很多的理论公式(我们在成核理论部分会了解到),但在工程应用过程中,我们更习惯通过宏观流体力学来分析表征,NANOscientific的源技术Flat-Foil就是结合的微观成核动力学和宏观上的流体力学无量纲数——雷诺数、斯特劳哈尔数和空化数来控制微米气泡的数量和尺寸的。
(6)计算流体力学模拟(CFD)
随着流体力学模型不断优化,以及计算资源的飞速提升,计算流体力学(CFD)以湍流平均运动方程(RANS)为基础,可以一定程度上模拟湍流过程,同时在人为加入实验得到的传质系数,CFD可以对微纳米气泡发生过程的两相湍流过程以及微米气泡强化传质过程进行模拟,另外,对于大流域增氧等大型工程,需要对增氧设备的排布,大流域留存进行模拟,以优化增氧设备放置位置、辅助流动方式等关键工程参数,NANOscientific在该领域有着非常丰富的工程经验,我们的CFD专家拥有超过20年的流体力学模拟经验(虽然两相流传质还是不咋准),可以在技术咨询和产品开发过程中发挥计算机模拟的优势,指导开发方向,减少开发工作量,缩短开发周期。
2.2 表面张力
我们先给出专业的表面张力解释,表面张力是指液体保持凝聚相,避免相坍塌分解为蒸汽而能承受的最大切向应力横向作用的超压分布积分。
别闹了,这会让大多数人关掉网页的。我们从刚才了解分子间作用力的思路来理解液体表面张力。对于空气中的液体,液体内部的分子被周围大量液体分子均匀包围,各个方向的分子引力相互抵消,合力为 0,分子处于受力平衡状态,而液体表面的分子,上方是密度和吸引力都很弱的气体分子,下方是液体分子,因此,表面分子仅受到向下(液指向体内部)的净吸引力。这种 “向下的净引力” 会将表面分子 “拉向” 液体内部,导致液体表面自发收缩,最终形成 “表面积最小化” 的趋势,这就是液体表面张力的本质。热力学上,恒温恒压下,增加单位表面积所需的可逆功,就称为即单位表面积的表面自由能。显然,影响液体分子间作用力的因素就会影响表面张力,例如液体分子之间的作用力越强,表面张力越大。对于液体中的气泡,由于该表面张力指向气泡,导致气泡由于表面张力额外增加了一部分压力,这部分压力就是拉普拉斯压力。
![]()
一提到微纳米气泡,无论是各种网站、AI答案、会议报告,“气泡内部压力高”、“表面张力引起的拉普拉斯压力”…,这些内容几乎从来不会缺席,因此每位客户几乎多多少少都知道了表面张力和额外压力,这也说明表面张力对于关注微纳米气泡的我们有多么的重要。在这里,作为专注微纳米气泡技术的我们,需要再深入了解一下表面张力,而不是只停留在几个“粗犷”的经典力学方程上,要知道,拉普拉斯推出方程的过程非常简单,是基础的经典力学,但其液体密度一致性、“微粒”间无结构、微粒处于完全静止状态…,这种假设非常粗暴(虽然随后经典力学的顶级专家瑞利也对此做出了优化调整),而我们平时挂在嘴边的,还是这些200年前的经典力学方程。他们在应用过程中没有过多错误,因为拉普拉斯分子“凝聚力”假设是和实验直接测定的“表面张力”挂钩的,所以不会发生多大的问题。但是,当热力学和统计力学出现,并用于研究表面张力时,问题就出现了。我们后面会了解到热力学和统计力学就会知道,分子是运动的,分子动能是一种统计分布,这种统计分布和概率性,在体相内由于空间对称性等可以忽略不计,但是表面能(张力)本身就是描述表面势能和体相分子势能差异的量,这恰恰说明表面分子的能级分布概率和体相相比存在不可“中和”的缺陷性“偏移”。
我们还是以一个简单的例子来解释这个过程以方便大家理解,例子可能有点“变态”,但却很形象。我们想象一个浴室(男女就不强调了,反正是同样性别的一群人),这个浴室是坐落在上海人民广场的,这是刚好十一黄金周,里面充满了洗澡的人,当然外面逛街的游客更多,人山人海,这时,浴室整个建筑突然消失了,会发生什么呢?为了减少“走光”人数,这些浴室里的人就会全部挤在一起,而且会很快变为圆形,因为人数相同的时候,占据的体积一样,圆形的表面积最小,也就是被游客看到“光屁股” 的人数最少。好,这是我们来分析这些人,只有不是最外层的,就没有“走光”风险,他们不着急,就那么站着,但最外面的人着急,想把身子挤进去,避免走光,这样,整个人群就受到了最外层向内的压力,如果把每个人看做分子,这个力就是拉普拉斯压力。
拉普拉斯就是这样简单计算出这个额外力的,但是,拉普拉斯把人看做是“死的”,但人实际上是活的,那活的人又会对这个过程产生什么影响呢?
首先,在最外层的人不会永远在最外层:因为最外层的人发现,光挤没有用,如果我憋口气,牟足劲趁着里面的人不注意,把他(她)弄到我外面来挡住我,我就“安全”了,这还会出现更极端的情况,当力气用的过大时,被拉出来的那个人整个都飞出了人群,这样不光屁股,前面也曝光了,这必然会让他(她)急迫不已,以最快速度回到人群里,只是能少曝光正面,如果刚好撞到一个力气不那么大的人,就直接挤进去了,整个人都安全了。
刚才我们说的是局部表面上一个往里挤和一个被挤出来的人的过程,我们想象一下,实际这个过程是同时发生在整个外表面上的。如果这是有位游客升起一架无人机,看记录这个人群的变化过程,我们可以看到人群表面是存在波动的(挤来挤去造成的)。
这个挤来挤去的过程,就会(我们这里用一个非常高级、非常专业的非平衡态热力学词汇)“耗散”死人形成的拉普拉斯力,或者换句话说,死人形成的圆形人群,外表面是刚性、连续的,而活人形成的圆形人群,外表面是柔性、不连续的。前者形成的表面张力可以用“粗犷的”、“没有人性的”经典力学方程直接给出,而如果将这些方程用于后者,就要分情况了。那么我们来看下有哪些情况:如果这个浴池只有几个人,那么这几个人会发现,彼此靠着还不如趴着,甚至不会形成人群,更不用说圆形人群了,也就是说,如果分子数量不足,是不会表现出宏观表面张力的;那么我们把人数增加一些,至少大家觉得要形成人群减少群体曝光度了,但形成的人群面积还很小,这种表面波动在无人机看来就会显得非常剧烈,整个人群呈现出不规则变化,这种不规则变化会令表面张力在宏观上失效;我继续增加人数,人群的尺寸足够大后,表面波动在无人机看来就就显得不那么剧烈了,而人群整体上基本呈现圆形,这是就可以使用经典力学方程计算表面张力了,但是我们必须像范德华修正克拉贝龙方程一样,需要在拉普拉斯给出的分子凝聚力系数上减去一个因为“人性”而产生的这种表面波动对“没有人性的”表面张力的衰减;我再继续增加人数,让人数非常多,这时,那这个圆形人群的半径会非常大,无人机上已经没办法分辨出外圈的这种波动了,这时,我们可以说因为“人性”产生的表面波动作用已经非常弱,可以忽略了,我们也就可以直接使用“没有人性的”经典力学方程了。上面的分析我们注意到一个细节,在人数增长过程中,我们把人数增长到可以使用负修正过的拉普拉斯方程计算表面张力时,得到的表面张力比我们平时直接用“没有人性的”经典力学方程算出来的小,也就是说人群受到的指向内部的压力小,这能不能用来解释我们关注的纳米气泡稳定性呢?看来也没啥不行的,我们试着“瞎编” 一下我们自己的纳米气泡稳定性理论:当气体分子由于局部过饱和开始析出,并逐渐聚集成比纳米气泡小的“超级纳米气泡”时候,由于“人数”不够,根本谈不上表面张力,“超级纳米气泡”向无人机看到的人群一样,呈现随机变化的不规则形状,长大或衰亡,既然我们知道液体中是讲究热力学和统计力学的,必然有选择长大的气泡,这是就像增加人数的浴池一样,进入到纳米气泡这个尺度后,表面张力开始有作用了,但这时的表面张力比我们平时直接使用拉普拉斯方程给出的要小很多,所以“纳米气泡” 其实没有没受到我们以为的那么大的挤压,轻松的很,它们继续遵循热力学和统计力学选择长大或者衰减,那么为什么宏观上“纳米气泡” 活那么久呢?后面我们到了胶体稳定性理论部分就知道了,作为气体分子组成的“疏水性”胶体,纳米气泡会形成表面电荷(这与实验结果一致,zata电位为负值)。我们可以直接借助DLVO胶体稳定性理论来解释纳米气泡稳定性,那么纳米气泡为什么又会消失呢,这就更容易了,直接给出奥斯瓦尔德熟化理论。
2.3 水的溶剂化
溶剂化是溶液化学的核心过程,指溶剂分子与溶质分子(或离子)通过相互作用形成稳定 “溶剂化复合物” 的现象,其产生的宏观影响,如溶解度提升、反应活性改变等称为溶剂化效应,例如,溶解在水中的气体分子作为 “溶质”,也会存在溶剂化作用。溶剂化的本质是 “溶质 – 溶剂相互作用” 与 “溶剂分子重新排列” 的协同过程,核心驱动力是系统 Gibbs 自由能(ΔG)的降低(熵驱动和焓驱动) —— 通过打破部分溶剂分子间的原有作用(如水分子间的氢键),同时形成更强的溶质 – 溶剂作用(如离子 – 偶极作用),最终使溶液达到能量更低的稳定状态。例如,气体分子溶解在水中时,首先要打破原有气体分子之间的作用力(实际上根本忽略不计),产生了自由能变化ΔG1,然后进入水中,破坏水的原有结构,产生自由能变化ΔG2,最终生成“溶剂化”溶气水,产生自由能变化ΔG3,如果这三个变化的和ΔG<0,则气体溶解自发进行,当然这里的ΔG= ΔH-T ΔS,整个过程是熵驱动还是焓驱动需要具体分析。
直接的静电力引发的静电相互作用会强化溶剂化,如溶剂是离子,而范德华力引起的溶剂化相对较弱,这些在分子间作用力部分已经详细了解过了。
我们通常使用溶剂化自由能(ΔGsol) 来定量表征溶解化过程的(溶质从真空转移到溶剂中的自由能)变化,负值越大,溶剂化越稳定)。这里我们简单介绍一下使用较为广泛的溶剂化自由能方程,其主要是将溶剂化自由能分解为静电项、孔穴项、色散项和氢键项, ΔGel为静电溶剂化能,极性溶剂中贡献最大,ΔGcav为孔穴,形成溶剂孔穴的能量,恒为正,非极性溶剂中占比更高, ΔGdisp为色散能,范德华力的主要贡献,非极性溶质 – 溶剂中起主导作用,恒为负,ΔGH-bond为氢键能,仅当溶质 、溶剂含氢键供体 、受体时存在,负値表示稳定。
溶剂化会影响溶质在溶液中的有效浓度(活度),对于稀电解质溶液,Debye-Hückel 理论通过描述 “离子氛”(溶质离子周围的反电荷溶剂化层)量化溶剂化对活度的影响:德拜——休克尔Debye-Hückel 极限公式(电解质溶液的活度系数)。该过程对于微细气泡的形成和稳定性有一定的影响,非极性气体受到离子氛抑制,降低溶解效率,而极性气体则与离子氛存在竞争一般会出现溶解度拐点。进一步地,离子氛也在一定程度上可以解释盐溶液中气泡稳定性。
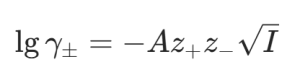
宏观连续介质到微观分子模拟,溶剂化理论的发展始终围绕 “更精准描述溶质 – 溶剂相互作用” 展开,核心模型分为连续介质模型和分子级模型两大类,例如通过求解泊松方程的极化连续介质模型(PCM)用于描述溶质-溶剂相互作用,而分子级模型包括分子动力学(MD)、从头算分子动力学(AIMD)等,实际上分子模拟在超细气泡(纳米气泡)稳定性的研究上发挥了非常大的作用,但在使用模型时,一定要考虑气液界面电介质不连续性,以确保模拟结果的可靠性。
