1.1 理想气体状态方程
由于我们讨论的气泡主要是由气体分子构成的,所以,我们先了解气体开始我们的内容。气体的研究已经有几百年的历史,从纯经典力学推导到引入热力学、统计力学,再到量子修正,包括大量的研究内容和理论分支,针对很多没有相关技术的背景客户在咨询过程中对气体的疑问,以及为后续理论知识介绍建立基础,我们主要来了解描述气体宏观性质的气体状态方程以及探究微观本质的分子运动理论和分子间作用力理论。
气体的宏观性质是指我们可以通过实验直接测量的物理量,如压强、体积、质量、温度等,根据实验结果建立这些物理量间的关系(数学模型),并最终形成一套完整的理论体系。
首先,玻意耳通过实验发现,当实验过程中温度(T)、物质的量(n)不变时,气体压强(P)与体积(V)成反比,数学表达式为:PV=C1
随后,查理通过实验发现,当实验过程中体积(V)、物质的量(n)不变时,气体压强(P)与绝对温度(T)成正比,数学表达式为:P/T=C2
再后,盖 – 吕萨克通过实验发现,当实验过程中压强(P)、物质的量(n)不变时,气体体积(V)与绝对温度(T)成正比,数学表达式为:V/T=C3
将上面三个实验结果整合到一起,可以得到一个更为完整的数学表达式:PV/T=C
随后,通过使用不同的气体、在不同的条件进行大量实验,拟合得到上述方程的常数C的值,结果发现,无论什么气体,C值都近似等于气体的总摩尔量的8.314倍,人们将这个8.314称为普适气体常数,记作R,这就是我们比较熟悉的理想气体宏观状态方程:
PV=nRT
1.2 分子运动理论
气体宏观性质的状态方程让当时的人们开始推断气体压强的本质,当时科学界高手如云,顶级专家都一致认为容器壁对气体分子的排斥力是压强的来源,只有一个微弱的声音认为气体压强是气体分子不断碰撞容器壁的宏观表现,曾被嗤之以鼻的贝努利最终开创了分子运动理论,他将气体看做是大量无规则运动的微小粒子构成,这些粒子完全弹性碰撞容器壁过程的动量变化可以得到和玻意耳实验结论一致的数学模型。
但贝努利的理论解释不了查理和盖 – 吕萨克的实验结论,因为这些结论表明这些“微小粒子”的运动能力与温度有关。更让科学“迷思”的是,一直使用的“温度”到底是啥?温度和气体运动能量为什么会有联系?难到说我们测量的温度在某种程度上就是气体运动能量的某种表现?
在这种情况下,气体运动理论的创始人之一麦克斯韦乘着七彩祥云来了,在查理和盖 – 吕萨克的实验结论的基础上,基于经典力学推导出了气体分子均方根速度分布公式:
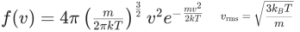
我们注意到,这个方程中气体分子均方根速度和温度的关系是基于查理和盖 – 吕萨克的实验结论的,方程并没有给温度的解释。
要实现温度本质的描述以及宏观温度与微观分子速度分布关联,还需要等待社会经济发展以及几位高手和一门学科的出现,随着工业革命的如火如荼,热力学也走上快速发展的道路,卡诺为了提高生产力,开启了关于热的研究,他发现咋的也不能让热都转化为功能,在卡诺研究的基础上,克劳修斯引入 “熵(Entropy,符号S)” 的概念,定义为 “可逆过程中热温熵的变化‘’,即系统进行可逆过程时,S不变,玻尔兹曼从统计学上出发,认为既然平衡态是最终状态,S不变,达到最大极值,那么对于整个系统内的分子肯定应该是处于最大可能的分布状态(最概然分布)的情况,最终得到终极方程,表明在热平衡状态下,微观粒子在不同能量状态上的分布概率,其本质是 “能量越低的状态,粒子占据的概率越高”,且分布概率与能量的指数函数负相关。

这个过程很多客户都不能理解,但我们通过一个简单的例子可以很形象的说明这个关系,先不管是不是恰当大,但所有人都懂了,这个例子是这样的:
一个小镇上,有5个饭店ABCDE,每个饭店能接待的人数都是6人,饭店菜品质量从A到E越来越差,我们把微观气体分子的分布看做一到吃饭点,人们在饭店的分布;
当镇上没有其他人,只有25个游客来到小镇时(我们看做是非平衡态),由于游客不知道菜品质量,分布是随机的,什么情况都有可能,但如果是非常熟悉小镇的客人(平衡态),最大可能性分概率分布应该是A6人,B6人,C6人,D6人,E1人。
超低温引发的气体分子能量分布偏移均分定理需要进行量子修正,将气体分子运动理论研究进入了量子阶段,这超出了我们需要了解的范围。
1.3 分子间作用力
1873年,快要延期毕业的范德华写完了在自己《论气体与液体连续性》的论文。范德华使用最简单的模型假设,推导出了实际气体状态方程以及分子间作用力公式,这使得分子间力被永久性的称为范德华力。范德华研究的崇高地位也彰显了微纳米气泡研究者们的重要性,从某种意义上说,纳米气泡研究者们也正在撰写一部《论气体与液体不连续性》的论文,这其中原因,在下文中会有所提及。
在这篇论文中,范德华主要目标就是找到克拉佩龙物态方程出现偏移的主要原因和解决方案(可以看出选题对于博士有多重要),他指出,只需要额外引入一个考虑分子吸引力的内压项和实际分子显然占有体积的体积修正项即可,这就是著名的范德瓦耳斯状态方程:
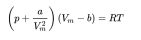
其中a代表分子之间的相互吸引力系数,b为分子的体积,a,b值可由实验测定的数据确定。这个方程不仅可以通过分子特征预测气体状态偏移,还可以预测判断临界温度,临界体积,临界压强等气体性质。同时,方程还引发了分子间作用力的研究。
在这里,我们需要额外插几句,由于物理学很多理论方程式从无线稀释极限假设出发的,一旦遇到真实情况怎么办呢?范德华虽然很聪明,加入了修正项,但就像辩证法说的一样,这也让后续几百年的研究都走上了这条路,比如后面我们会了解到的DLVO胶体稳定性理论,先完美假设,然后遇到偏差就加修正项,再遇到偏差再加修正项,加来加去,理论模型面目全非,不确定越来越大,数学求解也越来越难,在偏离较远时,其实已经没有意义或者说失效了。例如在溶解气体过饱和溶液开始自发成核前,热力学的均匀性假设其实已经失效了。
分子作用力是决定物质凝聚态(气、液、固)、相变、溶解等宏观性质和过程的分子层面根源。我们不去了解三种分子间作用力之一,和我们关系不大的卡西米尔力,只关注另外两种非常常见的分子力间作用力:范德华力和氢键。
正如我们所说,无一例外,分子间力都是电磁相互作用,而分子间的电磁相互作用显然与分子的极性有关。根据两个分子的极性,范德华力也分为三种,对于两个极性分子,彼此因极性相互吸引,称为取向力(开索姆Keesom力),例如NH3分子之间的力,其中,两个永久偶极子(偶极矩分别为μ1,μ2在距离r处的平均势能为:
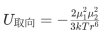
如果一个非极性分子靠近一个极性分子时,这个非极性分子内的电子会被极性分子“诱导”产生偶极矩,也就是说被诱导成了“半极性分子”,这样两个分子之间也就形成了吸引力,由于存在诱导过程,因此称为诱导力(德拜Debye力),如氮气分子溶解到水中的过程,永久偶极子(μ)对极化率为α的分子的势能:(α为分子极化率,反映分子被极化的难易程度,体积越大,α越大)。

如果一个非极性分子靠近另一个非极性分子时,两个分子还是相互吸引,宏观上让人费解。但从更小的时间跨度去分析,一个分子内的电子位置是量子化的或者说是不断变化的,因此从大的时间跨度上的非极性分子,在很小的时间跨度内时是具有微量极性的,称为瞬时偶极矩,两个非极性分子因瞬时偶极矩在很小时间跨度上的相互吸引力在大跨度时间上的累计就表现为吸引力,称为色散力(伦敦London力),如两个氮气分子之间的吸引力,两个非极性分子(极化率分别为α 1,α 2,电离均能近
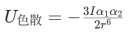
由于我们关注的气泡很多都在水中,因此我们还要简单了解一下氢键。氢键的形成条件:X-H…Y,其中 X(N/O/F)电负性大、半径小,导致 X-H 键极性极强,H 原子几乎成为 “裸露质子”,与 Y 原子的孤对电子产生强静电吸引,一个 H 原子只能形成一个氢键,X-H…Y的方向尽可能呈直线,以最大化静电作用,氢键键能通常为 10–40 kJ/mol,大于偶极矩作用引起的范德华力与电子质子相互作用的共价键。
